Designing a 16-bit Adder

This article is derived from a lab report during my student years and is recorded here for reference. The accuracy of the content has not been verified after the experiment.

Open Table of contents

Overview
16-bit Adder Design
Circuit Diagram
Timing Simulation Diagram
Conclusion

Overview

To construct a 16-bit adder, we can utilize Carry Lookahead Adder (CLA) components or full carry lookahead adders, connected in series. The 16-bit adder can be divided into groups of four bits, where each group uses a 4-bit carry lookahead adder, while the carry between groups is handled serially.

16-bit Adder Design

According to the full adder equations, for a 4-bit adder, the carry outputs $C_1, C_2, C_3, C_4$ are generated based on the following conditions:

\begin{align*} C_1 &= X_1 Y_1 + (X_1 + Y_1)C_0 \\ C_2 &= X_2 Y_2 + (X_2 + Y_2)C_1 \\ &= X_2 Y_2 + (X_2 + Y_2)X_1 Y_1 + (X_2 + Y_2)(X_1 + Y_1)C_0 \\ C_3 &= X_3 Y_3 + (X_3 + Y_3)C_2 \\ &= X_3 Y_3 + (X_3 + Y_3)[X_2 Y_2 + (X_2 + Y_2)X_1 Y_1 + (X_2 + Y_2)(X_1 + Y_1)C_0] \\ &= X_3 Y_3 + (X_3 + Y_3)X_2 Y_2 + (X_3 + Y_3)(X_2 + Y_2)X_1 Y_1 + (X_3 + Y_3)(X_2 + Y_2)(X_1 + Y_1)C_0 \\ C_4 &= X_4 Y_4 + (X_4 + Y_4)C_3 \\ &= X_4 Y_4 + (X_4 + Y_4)[X_3 Y_3 + (X_3 + Y_3)X_2 Y_2 + (X_3 + Y_3)(X_2 + Y_2)X_1 Y_1 + (X_3 + Y_3)(X_2 + Y_2)(X_1 + Y_1)C_0] \\ &= X_4 Y_4 + (X_4 + Y_4)X_3 Y_3 + (X_4 + Y_4)(X_3 + Y_3)X_2 Y_2 + (X_4 + Y_4)(X_3 + Y_3)(X_2 + Y_2)X_1 Y_1 + (X_4 + Y_4)(X_3 + Y_3)(X_2 + Y_2)(X_1 + Y_1)C_0 \end{align*}

From the equations, it is evident that each carry expression includes terms for $X_i + Y_i$ and $X_iY_i$ . To simplify this, we define two auxiliary functions:

P_i = X_i + Y_i \\ G_i = X_iY_i

Propagate Function ( $P_i$ ): This function indicates that when either $X_i$ or $Y_i$ is 1, if there is a carry-in from the lower bit, it will definitely be passed to the higher bit.
Generate Function ( $G_i$ ): This function indicates that when both $X_i$ and $Y_i$ are 1, regardless of whether there is a carry-in from the lower bit, a carry-out will be produced.

Using these definitions, we can express the carry-out as:

\begin{align*} C_1 &= G_1 + P_1 \cdot C_0\\ C_2 &= G_2 + P_2 \cdot G_1 + P_2 \cdot P_1 \cdot C_0\\ C_3 &= G_3 + P_3 \cdot G_2 + P_3 \cdot P_2 \cdot G_1 + P_3 \cdot P_2 \cdot P_1 \cdot C_0\\ C_4 &= G_4 + P_4 \cdot G_3 + P_4 \cdot P_3 \cdot G_2 + P_4 \cdot P_3 \cdot P_2 \cdot G_1 + P_4 \cdot P_3 \cdot P_2 \cdot P_1 \cdot C_0 \end{align*}

From the above expression, we see that each carry output $C_i$ depends only on $X_i$ , $Y_i$ , and $C_0$ . This means that there is no dependency among the carry outputs. As soon as $X_1$ to $X_4$ , $Y_1$ to $Y_4$ , and $C_0$ arrive simultaneously, the carry outputs $C_1$ to $C_4$ can be generated almost simultaneously, alongside their respective sums.

Circuit Diagram

To illustrate this concept, we can represent the wiring diagram for a 4-bit adder:

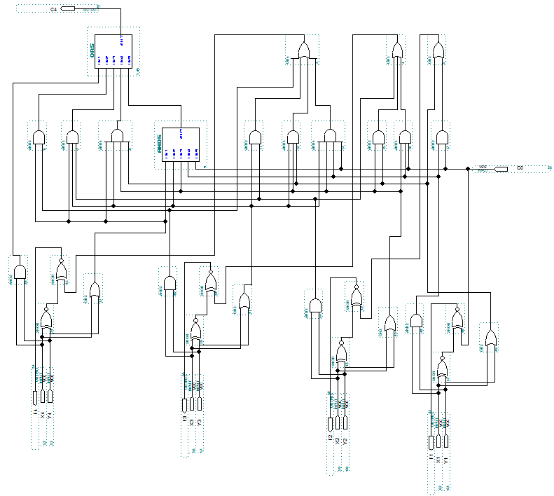
4-bit Adder Circuit Diagram

In total, for a 16-bit adder, we can connect four groups of 4-bit adders as follows:

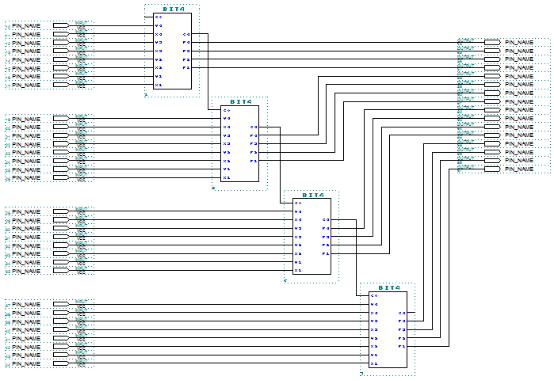
16-bit Adder Wiring Diagram

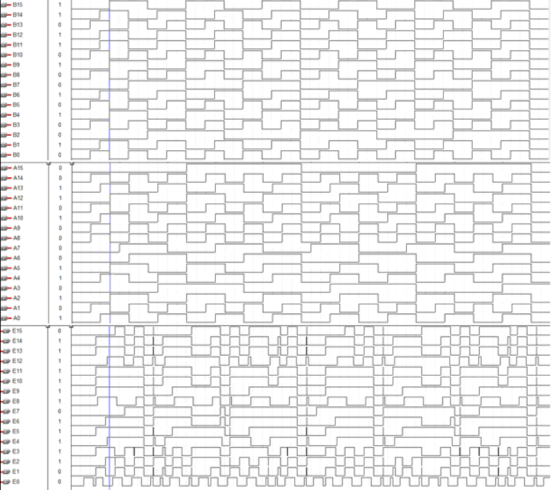
Timing Simulation Diagram

Below is a timing simulation diagram that demonstrates how the carry propagation and sum generation occur in a 16-bit adder:

16-bit Adder Timing Simulation Diagram

Conclusion

By utilizing the principles of carry lookahead adders, we can efficiently design a 16-bit adder. This modular approach not only simplifies the complexity of the overall design but also enhances performance through faster carry generation. By effectively dividing the adder into smaller 4-bit sections, we leverage the benefits of parallel processing within the groups while managing carry propagation between groups.